Getting the physics right in simulations

By Bas van ‘t Hof and Thea Kik-Vuik

In the simulation of physical processes, some important physical property may get lost due to the computational method. For example, energy loss can be introduced in a simulation of a process that is not supposed to lose energy. Recently, we published new computational methods that avoid such problems. These conservative discretizations conserve certain physical quantities like mass, momentum, and energy, or all at the same time. This means that our methods make simulations more accurate and more reliable.

Why is the conservation of physical quantities important?

Conservation of mass, momentum and energy is very important to accurately simulate physical processes. If the computational method that is used in the simulation does not conserve energy (or mass, or momentum), then simulations can fade away or become unstable, see for example the figure below.

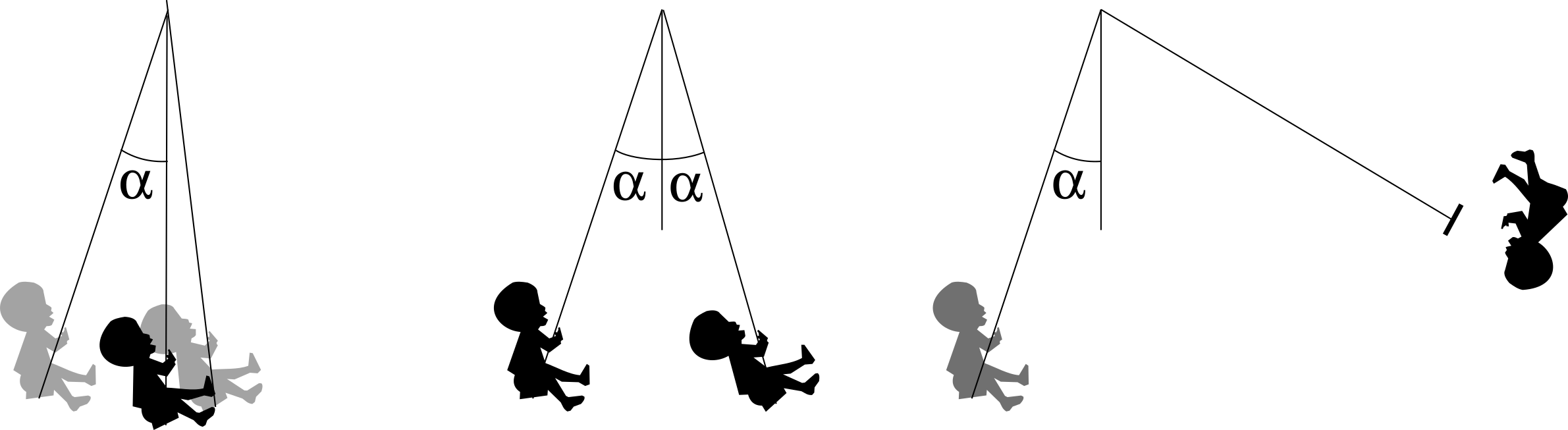
A good example of an application that is sensitive to this effect is the simulation of turbulent flows. Turbulent flows are everywhere: in the air, in water, but also in many industrial applications. These flows are described mathematically by the so-called Navier-Stokes equations.

Detailed numerical studies of turbulent flow can be carried out using large-eddy simulation (LES) or direct numerical simulation (DNS). In both cases, the turbulence is determined by the so-called energy cascade. This means that the kinetic energy of the main flow is transferred to that of the large eddies, and from there to smaller eddies. In the smallest eddies, the velocity differences are so large that the kinetic energy is dissipated into heat. To properly simulate such turbulent flow, it is important to properly compute the energy cascade. We need to avoid instability (which would blow up the solution) and artificial dissipation (which would cause the solution to fade away).

Energy conservation is also very important in predicting earthquakes. The amount of damage is mainly dependent on the seismic energy of an earthquake. Therefore, calculations that apply seismic energy are more useful than the ones that use seismic moments. Again, proper computation of the energy in the model is crucial.

Also in the oil and gas industry, energy conservation is important, for instance in exothermic processes in oil wells and in the corresponding reservoir simulations. Similarly, conservation of mass, momentum and energy is necessary for the numerical computations behind seismic technologies used for oil and gas exploration. This is because the sound-wave equations are described by energy-lossless wave equations. If there were any artificial or numerical dissipation at all, then the solution would fade away altogether; if there were any kind of instability, it would blow up.

One more example for which energy conservation is important, is in computations involving shallow-water equations (see also Wikipedia). For this application, Guus Stelling invented a method that conserves either momentum or energy, locally, by choice. That’s a big step, but our new method goes even further as it conserves both energy and momentum at the same time.

All these applications are real-world examples where the computational method can make or break the value of the simulation.

Where does it go wrong?

For each real-world phenomenon (such as in the examples above), a mathematical formulation or mathematical model can be made, that is: a set of equations that describe how the process evolves in time. To do computations with such a model, it needs to be reformulated into a form that can be handled by a computer. This new formulation is called the discretization of the continuous model, reflecting the fact that computers can only deal with discrete steps rather than something that is continuous.

In the resulting discrete model of the phenomenon, the (continuous) differential operators in the original model have been replaced by (discrete) difference operators. Unfortunately, not all properties of these differential operators are automatically inherited by their discrete approximations. For example, symmetry and positiveness may be lost in the discretization process. Also, mass, momentum, and energy may not be conserved.

The solution: conservative discretization methods

Symmetry-preserving methods, or mimetic methods, aim to conserve (or preserve) certain properties of a continuous differential operator in its discrete counterpart. In our paper, we present a new symmetry-preserving discretization technique. For those who are familiar with the terminology of numerical mathematics: it is a finite-difference symmetry-preserving discretization of arbitrary order on structured curvilinear staggered grids.

Our new method is obtained by writing the discrete equations in a special form. Here, we separate the easy (linear) parts from the difficult (non-linear) parts. These parts of the equation should all satisfy certain properties (related to so-called null spaces, symmetry, and self-adjointness). In our paper, we describe the corresponding discretization method that satisfies all requirements.

Next to the conservation of mass, momentum and energy, the resulting method also yields a meaningful adjoint operator. This has advantages for accuracy and stability in optimization problems.

What’s different in these conservative discretizations?

The methods that we found in the literature are not at the same time applicable for arbitrary discretization orders, curvilinear staggered grids, and sophisticated operators. Or they are not able to conserve mass, momentum, and energy together.

The novelty of our work is that it combines

• arbitrary order of convergence (a property related to accuracy),
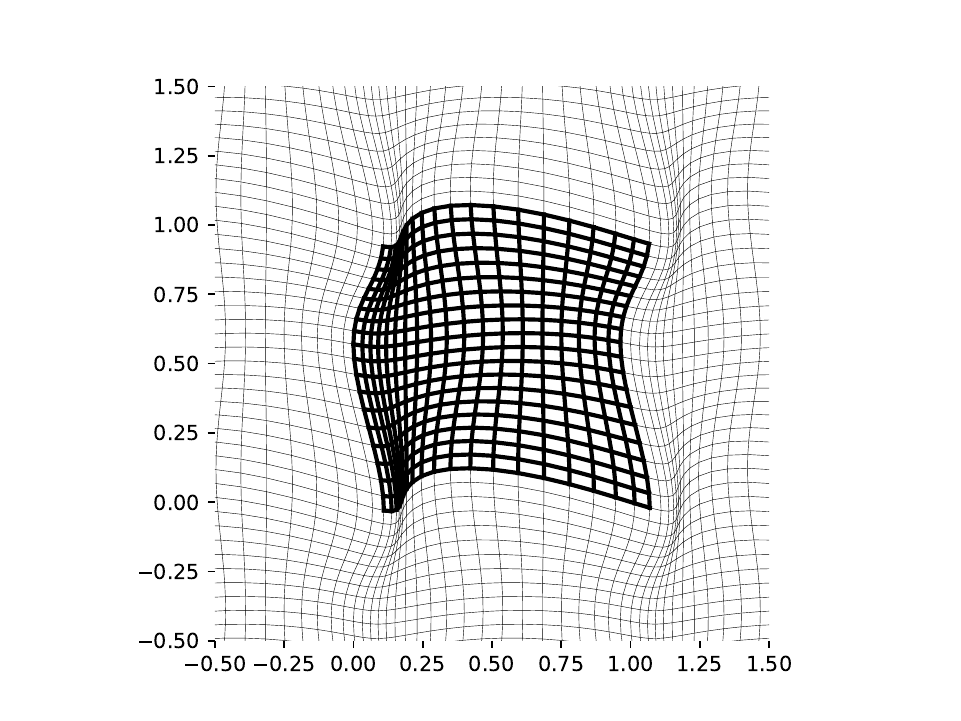
• orthogonal and non-orthogonal structured curvilinear staggered meshes (see figure below), and
• the applicability to a wide variety of phenomena, such as the shallow-water equations, earthquakes, and turbulent flow, while conserving mass, momentum, and energy.

Work in progress

Some of the techniques are already successfully applied in projects of our clients. For example, the research was inspired by calculations that are done by Rijkswaterstaat.

During the ECCOMAS conference in 2021, we heard about another trick that might be useful to obtain similar results, which we will certainly investigate. At this moment, we are mainly working on a time-integration method (as opposed to the discretization method) that also conserves mass, momentum, and energy.

At VORtech, we have several people that apply these kinds of complex mathematical techniques in their daily work. Although we are mostly focused on making computations work for our clients, we also take some time to do more fundamental research when we see that it benefits our clients.