Study Group Mathematics with Industry 2017

The Study Group Mathematics with Industry (SWI) is an annual workshop event in the Netherlands. During one week, roughly 50-80 theoretical and applied mathematicians work together in groups on complex problems posed by industry. These problems are usually of practical interest and tough to solve. Later this year, the proceedings of the SWI, with the solution approaches of each group, will appear.

This year the Study Group Mathematics with Industry took place in Amsterdam, from January 23 till 27. Bas van ‘t Hof and Jok Tang, two of VORtech’s mathematical consultants, attended the SWI this year. At VORtech, they work on complex problems, algorithms, and scientific software for clients. They attended the SWI, because they were eager to work on new problems, to interact with fellow mathematicians, to compare their approaches with others’, and to learn new stuff.

Bas van ‘t Hof worked on the Shell case called “numerical-physical modelling of miscible fluids in pipeline transport”, while Jok Tang worked on the ABN AMRO case called “the fair value of a mortgage”.

The Shell case: modelling of miscible fluids in pipeline transport

The problem posed by Shell dealt with the flow of two fluids in a pipe line. The difference in density of the two fluids makes them flow at different speeds, and diffusion causes mixing of the two fluids. When injecting the second fluid to a pipe filled with the first fluid, the flow may allow certain parts of the pipe to be ‘untouched’ by the second fluid, for instance in the recirculation area at the bottom of a bend in the pipe, as can be seen in the following figure.

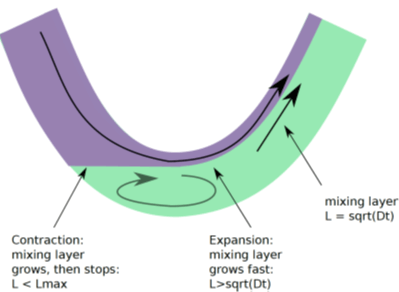
Pipe flows are among the most-studied phenomena in the world of mathematical modelling, so it was essential to ask the problem owners precisely what they already knew about the flow and what they still would like to know: it was clear that a complete solution of everything would be out of the question.

It turned out that a good understanding of the non-mixing flow was available, because the flow could be stitched together from a number of so-called Taylor bubbly flows. The SWI work group of Bas then suggested two approaches to obtain an understanding of the effect of mixing:

• Asymptotic analysis for small diffusion parameter;
• Setting up a 1D model, calibrated so that it is correct for the non-mixing case.

Both approaches were followed and seemed successful. A preliminary result with some characteristics of the mixing effect was obtained (see the figure above), and some numerical results were presented from the 1D model.

Fine tuning and validation of the models, even scanning the models for errors in the derivation or mistakes in the assumptions are still to be done for both approaches.

Bas: “It was exciting to see what a few people can come up with in only a few days, when they study a problem that is by no means uncharted territory.”

The ABN AMRO case: determining the the fair value of a mortgage

The problem posed by ABN AMRO dealt with mortgages. Mortgages are an important part of the bank’s core business model. They can be seen as loans, and cover about 40% of the total assets of the bank. In order to properly steer the balance sheet and manage the bank’s risks, it is essential to correctly estimate the cash flows resulting from mortgages.

Mortgages come with so-called embedded options for the client, which make the determination of the mortgage’s value a complex task. A typical option is called prepayment: the client is allowed to repay (part of) the loan earlier than he would be required to do.

The amount of money borrowed and paid by a client with a mortgage contract may look as follows.

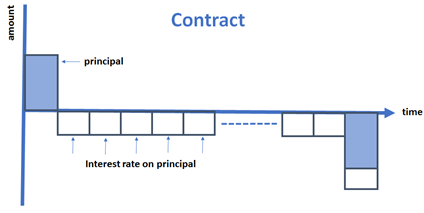
The client may decide to sell the house, so that he can use the money to pay-off the mortgage. In this case, we have the situation as described below.

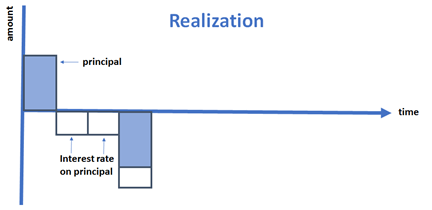
This is a risk for the bank, as it will not receive all planned interests in the future, see the red boxes in the next figure.

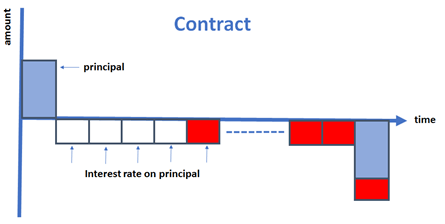
The challenge is to include predictions of prepayments appropriately into the bank’s current models. With these models, the value of a mortgage portfolio with (random) prepayments can be calculated more accurately, which is beneficial for the bank.

Jok’s SWI work group studied several aspects of the problem and came up with three approaches:

• Prepayment implementation approach, where future prepayments are projected based on prepayments done in the past;
• Approximate closed-form expression, where probabilistic techniques and Taylor-series approximations are used to compute the net-present value of each contract;
• Multidimensional interpolation, where the present value is determined by simulation and the probability of prepayments is determined based on clustering of past data points.

The three approaches are complementary, and could be used separately, partly together, and combined.

Jok: “Working in such a study group was inspiring. There was a good interaction between the group members. And, although the problem was tough, we have managed to do some good data analysis, and came up with both mathematical and implementation approaches that could be useful to the bank”.

Final thoughts

The new approaches were well-received by the companies, according to the positive feedback delivered by them during the final day.

Both Bas and Jok were inspired by working with other scientists, especially the young generation of mathematicians, during the Study Group Mathematics with Industry. The workshop was a good way to improve the skill sets and to keep in touch with academia. Fellow mathematicians are encouraged to participate in future editions of this annual event.

If you work at a company and you have a mathematical challenge, you can pose it as a problem for the Study Group Mathematics with Industry. Please see the SWI website for more details. Of course, you can contact VORtech, if you need a dedicated mathematical or scientific software solution for your problem.